Comentario:
este tema de ecuaciones de primer grado, no entendi mucho, porque en realidad yo no aprendí bien a resolver las ecuaciones y como en este tema para allar el resultado que se quiere se deben hacer ecuaciones, por ese motivo se me hace muy difícil resolver los problemas. Pero trataré de ver quien me enseña a resolver las ecuaciones, ya sabiendo las resolver, no me costara allarle la solución a cada problema, y la verdad que si le parese muy interesante este tema.
Contenido en el cual nos habla de que son las ecuaciones de primer grado.
Ecuaciones de primer grado o lineales
|
Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).
Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1. Se reducen los términos semejantes, cuando es posible.
2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.
3. Se reducen términos semejantes, hasta donde es posible.
4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.
Ecuaciones de Primer Grado
Ecuaciones de primer grado, es una
simetría de dos expresiones, donde está presente una
incógnita cuyo valor puede ser relacionada a través de operaciones aritméticas. Se llaman ecuaciones de primer grado si el exponente de la incógnita es uno.
Para resolver una ecuación de primer grado, los términos deben cruzar de un lado de la ecuación al otro, de modo que todos los términos con la incógnita estén en un lado y los otros en el otro, tomando la precaución de mantener la igualdad de expresión.
La ecuación literal de primer grado, contiene expresiones literales además de la incógnita. Por convención, las últimas letras del alfabeto se identifican como incógnita y, literalmente, como las primeras letras del alfabeto (se supone que estos literales son valores constantes).
Esta cantidad desconocida es la incógnita, que generalmente se designa con letras minúsculas de la parte final del alfabeto: w, x, y y z; las letras iniciales minúsculas del alfabeto: a, b, c. Dichas ecuaciones de resolución representan una solución cuyo nombre llamaremos raíces de la ecuación a los valores de lo desconocido que cumplen con la igualdad
Ecuaciones de primer grado
En esta página vamos a resolver
ecuaciones de primer grado paso a paso. Comenzaremos con ecuaciones muy simples e iremos aumentando su dificultad. En las ecuaciones tendremos sumas, restas, productos y cocientes de monomios sin parte literal (es decir, números) y de monomios con la parte literal
x (como
2x ó
3x2).
Resolver una ecuación consiste en encontrar el valor que debe tomar la incógnita
x para que se cumpla la igualdad. Podemos comprobar si la solución encontrada es correcta sustituyendo la incógnita
x por la solución. Como regla general, una ecuación de primer grado tiene una única solución. No obstante, puede darse el caso de que
no exista ninguna o que existan infinitas(veremos algún ejemplo de estos casos).
Enlace:
Ejer
Ecuación 2
Solución
Escribimos los monomios con incógnita en la izquierda y los que no tienen incógnita en la derecha.
Como
5x está sumando en la derecha, pasa restando a la izquierda. El número 1 de la izquierda está restando, así que pasa sumando al otro lado:
Sumamos los monomios en cada lado:
Es decir,
Para despejar la incógnita, debemos pasar el coeficiente de la incógnita a la derecha. Como está multiplicando, pasa dividiendo (con el signo negativo incluido):
Finalmente, simplificamos la fracción:
Por tanto, la solución es
x=−3.
Comprobamos la solución sustituyendo en la ecuación:
Ecuación 3
Solución
Escribimos en la izquierda los términos que tienen la incógnita y en la derecha los que no la tienen:
Simplificamos ambos lados:
Hemos obtenido una obviedad. Esto significa que la incógnita puede tomar cualquier valor. Por tanto, todos los números reales son solución de la ecuación:
Comprobamos que la ecuación se cumple para cualquier número. Sustituimos, por ejemplo,
x=1 en la ecuación:

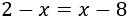
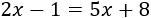
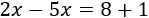
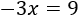
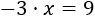
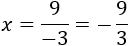
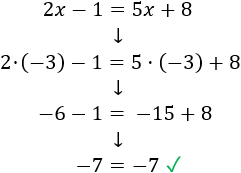
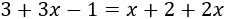
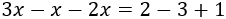
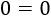
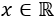
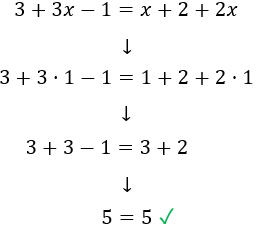

Muy bien, cualquier duda me puede consultar. Saludos
ResponderBorrarEsta bien. Gracias lic
Borrar